仮説検定における「サンプルサイズ」「有意水準」「検出力」「効果量」とは何か

はじめに

業務で統計を使うことがあるのですが、統計は独学であるため、理解が足りていないことも多いです。最近仮説検定を使って分析を行っていた時に、目的とする変数は改善しているんだけれどもp値が有意じゃないということがあって、これってサンプルサイズをもっと増やして分析するのがいいんだっけ？でも、有意にするためにサンプルサイズ増やすのってよくないと聞いたことがあるな、となりました。

そんなことを考えているうちに、そもそも効果量ってなんだっけ？検定力ってどういう風に使うんだっけ？と疑問がわいてきまして、大雑把な理解はしていたつもりですが、調べて以下にまとめてみることにしました。

ちなみに自分は、データ系の職種についていますが、冒頭に書いたように統計は独学ですので、専門的な学習をしてきたわけではありません。ビジネスで統計を使う人間として、理解や解釈を踏まえてまとめていますので、ご了承ください。特に、一部は調べても明確には分からなかった部分があり、私見が反映されている部分もあります。

そもそも仮説検定とは？

Wikipediaを引用すると

仮説検定（かせつけんてい、英: hypothesis testing）あるいは統計的仮説検定 (statistical hypothesis testing) とは、母集団分布の母数に関する仮説を標本から検証する統計学的方法の一つ。

とあります。難しい言葉が並んでいますが、ある仮説を得られたデータから検証する方法のことで、例えば、WebUIに対してABテストを行った時、新しいUIは元のUIと比較してお商品のお問い合わせや申し込みが増えているのか？ある工場の不良率は他と比べて特別高いか？など、数字から客観的な判断を行うことが出来ます。

仮説検定のやり方は色々あるのですが、ビジネスでもよく使われるところでは、t検定とカイ二乗検定があります。

例えば、ある学校で同程度の学力の生徒の一部に補習を行ったとします。補習を行った生徒とそれ以外の生徒のテストの差が以下の通りだった場合、補習を受けた生徒は成績がよくなったと言えるのか？ということを調べたいとします。

補習を受けた生徒	補習を受けていない生徒
60	50
70	70
70	35
77	75
44	65
65	40
60	38
66	62
70	55
80	40

補習を受けた生徒の平均点はおおよそ66点で、そうでない生徒は53点です。直観的には差がありそうですが、これを客観的に判定しようとするときにはt検定が役に立ちます。

エクセルで検証を行うときは、T.TEST関数を使います。

=T.TEST(範囲1, 範囲2, 尾部, 検定の種類)

範囲1,2にはそれぞれグループごとのデータを、尾部と検定の種類は詳細は省略しますが、検証したい内容に応じて設定します。（今回は1,2を設定します。）すると、0.014934…という数字が出てきて、これはグループの平均点の差が偶然現れる確率を意味します。1.5%ですので、おおよそ、同じような検証を100回繰り返せば1,2回は偶然差が生じるという解釈になります。

p値は大体の場合で5%を基準とすることが多く、5%を下回っていれば、それは統計的に有意な差があるとみなしてよいと言われています。この5%には特に根拠はなく、慣習的に20回に1回ぐらいは間違いがあってもよいだろうという意味のようです（事前に有意水準は決めておく必要があります）。

検定の結果を決める4つの要素について

上の例で仮説検証のやり方とp値の見方を確認しました。ここまでは比較的メジャーな内容ではないかと思います（少なくともデータ分析に興味のある方にとっては）。では、冒頭で話した効果量や検定力とはどこに出てくるのかというと、主に事前のサンプルサイズの設計という文脈で出てくることが多いです。

まず、基本的な知識ですが、仮説検定の結果を決める要素には、「サンプルサイズ」「有意水準」「検出力」「効果量」の4種類があり、そのうち3種類が決定できれば、残り1種類の値は自動的に決定します。上で書いたサンプルサイズの設計は「有意水準」「検出力」「効果量」を、検出力を見たいときは「サンプルサイズ」「有意水準」「効果量」を決めれば、残りの「サンプルサイズ」や「検出力」の値が決まります。

「有意水準」は前項のp値の基準です。仮説検定を行った際に、何％を下回ったら有意であるとみなすかの基準になります。「サンプルサイズ」はそのままで、データ数になります。詳細は省きますが、仮説検証ではサンプルサイズが大きくあればなるほど、検定結果が有意になりやすくなります。検証したい仮説が、決めた有意水準で統計的に有意かどうかを検証するために必要なサンプルサイズはどの程度か？という風に使います。

「検出力」と「効果量」はあまり聞かない言葉だと思います。「検出力」は検証している要素に実際に有意な差があった場合に、有意な差があると検証できる確率です。「効果量」はその効果の大小を客観的な指標で表せるものになります。

「検出力」の説明はちょっとややこしいと思いますが、仮説検証の前提知識となる「母集団」と「標本」について、理解する必要があります。仮説検定では、ある「母集団」同士の効果の差が実際にあるかどうかを「標本」のデータを使って推測することにあります。ここで「標本」は「母集団」から一部を抽出しただけのサンプルデータでしかないため、「母集団」の情報を完全には再現できていません。そのため、「母集団」の結果からたまたま大きく外れた平均値が抽出される場合もあります。t検定の場合、この「母集団」の平均の分布を「標本」から確率分布的に表現したうえで、たまたま平均の差が生じている可能性がどの程度あるのかを計算します。これが前項で説明したp値でt分布の中でたまたま外れる確率が5%未満になっているかどうかを確認していることになります。

■仮説検証でp値が5%未満のイメージ

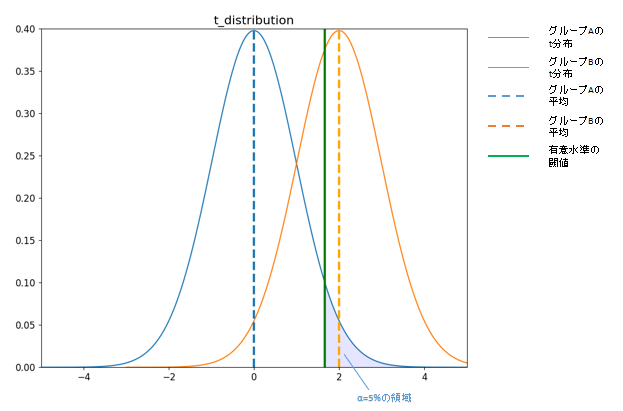
ここで大切になるのが、p値が5%という統計的有意性を確認できなかった場合に、グループ間に効果の差がなかったという意味ではないということです。p値が5%以上だった場合の解釈は、「検証したグループ間に効果の差がなかった、という可能性を棄却できない」というだけで、実際には効果があったかもしれないけれども、検証の結果からは分からなかった、ということになります。

この時、可能性としては二つ考えられます。それは、「本当は効果の差があるのだけれども、検出力が弱くて有意差が確認できなかった」のか「本当に差がないのか」です。「本当は効果の差があるのだけれども、検出力が弱くて有意差が確認できなかった」場合、効果があるものを効果がないと棄却してしまう可能性があり、そのような事象は第二種の過誤といいます（ちなみに、効果の差がないものを効果の差があるとしてしまう（＝p値の検証で有意と出てしまう）ことを第一種の過誤といいます）。

この「本当は効果の差があるのだけれども、検出力が弱くて有意差が確認できない」状態になる確率はβと表され、反対に1-βの値が「検出力」といわれるものになります。そして、「効果量」はt検定の場合、比較したい平均の差のことを表しており、詳細は省きますがCohenのdなど、単位の大きさに関わらずに指標化できる計算方法がいくつかあります。

■βの領域イメージ

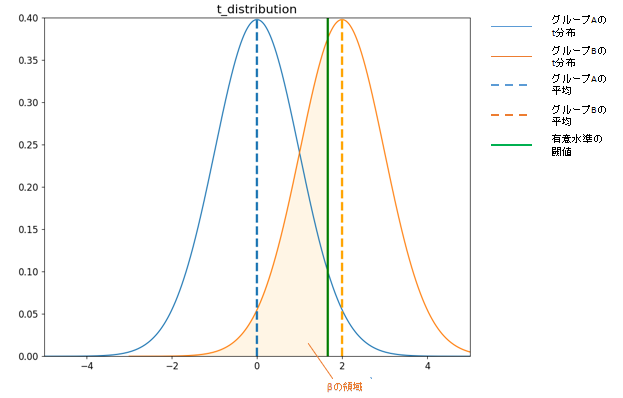
なお、検証結果が「本当は効果の差があるのだけれども、検出力が弱くて有意差が確認できてない」状態であるのかは、分析の結果からはわかりません。仮説検証でできることはあくまでも、統計的に有意であると言えるか言えないかであって、効果の差がないということを結論づけることは出来ません。

検出力は、おおよそ80%～90%で設定することが多いようです。これは、10～20%（1-検出力）程度は「本当は効果の差があるのだけれども、検出力が弱くて有意差が確認できなかった」ということを許容していることになります。検出力が低い場合、実際に効果があっても仮説検定での有意差が出にくくなります。

■仮説検定で有意差が出にくい（βの領域が広い）時のイメージ
βの領域の確率だけ有意差が出ない

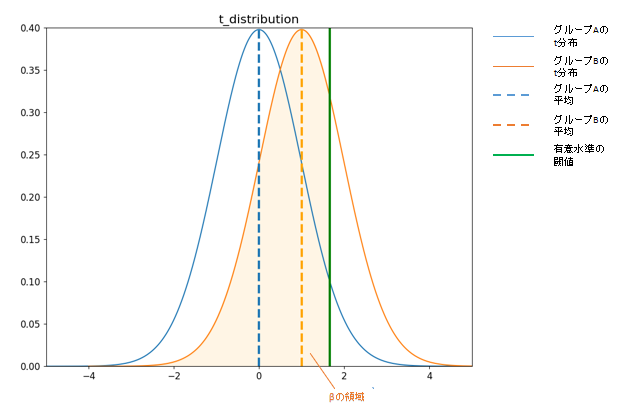
有意性を確認できなかった場合、どうすればいいのか？

ここから先は、かなり私見も含みます。いくつかの記事や論文を読んでみたのですが、簡素にまとめられて実例が書かれていなかったり、事後に検出力分析を行うべきと書かれていたりするのですが、あまり意味があるように自分には思えなかったからです。ここは理解の足りていないところもあるかもしれませんが、自分なりの解釈で記述します。

まず、有意差が確認できなかった場合、定義上、検出力は必ず50%以下になります。有意差が見られないのは検出力が足りなかったからだ、と主張するには、そのような結果が出てくることは当然だと思いますので無理があるように思われます。また、有意差が確認できた場合に検出力を確認したとしても、どういった意味があるのか自分にはわかりませんでした。

仮にサンプルサイズを事前に計算して、実験を行っていた場合、「本当は効果の差があるのだけれども、検出力が弱くて有意差が確認できてない」結果になる理由は、効果量が想定していたよりも低かったということになるはずです。有意水準は固定ですし、サンプルサイズが十分に集まっていたとしたら、検出力が下がる理由は効果量以外にないからです。ですので、差はあるけれども検出力が弱かったという可能性を考えるのであれば、実際に得られた効果量が意味のある差であるかを考えるのが最初になるのではないかと、自分は思いました。

実際に得られた効果量に意味があるかどうかは、ケースバイケースによるところが多いと思いますので、都度判断していくしかありません。例えば、ビジネスの領域であれば、その効果がコストに対して元が取れるか否かが一つの分水量になると思います。

意味のある効果量であると判断された場合、サンプルサイズを増やしての再検証というのが、おそらく、選択しやすい方法になるかと思います。今回調べていた中で検出力をあげる方法は他にもあるようでしたが、ちょっと理解不足なので、一番わかりやすい選択肢だけ書いておきます。この辺はもう少し理解を深めたいです。

ただ、冒頭で記載した、むやみにサンプルサイズを増やしてはならない、という考え方に対しては反論が出来ると思います。サンプルサイズをむやみに増やしてはならない根拠は、サンプルサイズの増加によって意味のないレベルの効果量を有意差ありと結論付けてしまうリスクを考えてのことですので、効果量に意味があるのであれば、そのリスクは問題がないと思われます。

まとめ

まとめると仮説検証の大まかな流れは、以下のように進めるのがよいのではないかと思います。

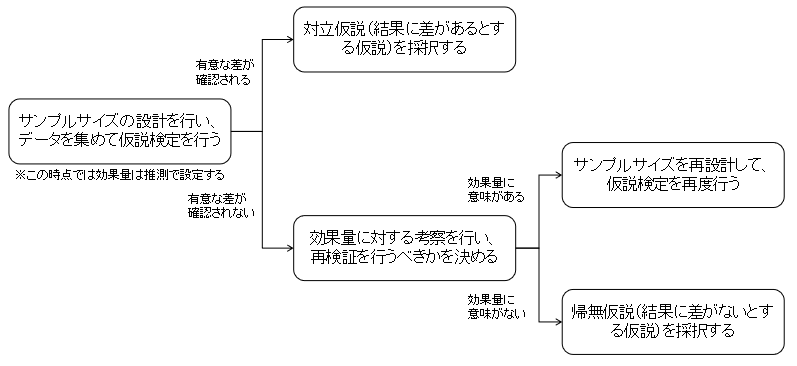
実際には、ビジネス上の制約や状況などによって、きれいにこの流れにならないこともあると思いますし、そもそも検証を何度も行うことはコスト的な観点でもあまりよろしくはないので、最初の設計をしっかりとやるべきだという考え方が正しいとは思います。が、うまくいかない場合の対応は頭に入れておいてもよいのではないかと思います。

改めて、このあたりのことを調べてみて、これまでp値を使ってなんとなく分析をしてきていましたが、奥深い分野なのだなと感じました。記事の途中でも記載しましたが、個人的に理解しきれていないと思えるところもまだまだありましたので、また勉強をして追記や修正などあれば、書いておきたいと思います。

読んでいただき、ありがとうございました。